Controlabilidad y Observabilidad
Orden del día
- Solución de preguntas.
- Diseño de controlador.
- Diseño de observador.
- Control integral.
Conceptos
- Controlabilidad
- Matriz de controlabilidad
- Observabilidad
- Matriz de observabilidad
- Posicionamiento de polos
Controlabilidad
Diagrama de bloques de un sistema en lazo abierto y lazo cerrado, con realimentación de estados.
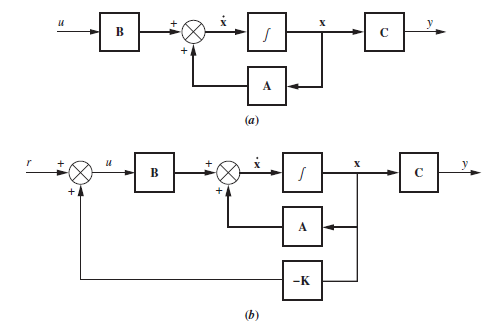
Para el lazo cerrado tenemos una representación en espacio de estados:
\[\begin{align} \dot{x}&=A\,x+B\,u=A\,x+B(-K\,x+r)=(A-BK)\,x+B\,r \\ y&=C\,x \end{align}\]Observabilidad
Diagrama de bloques de un sistema con estimador.
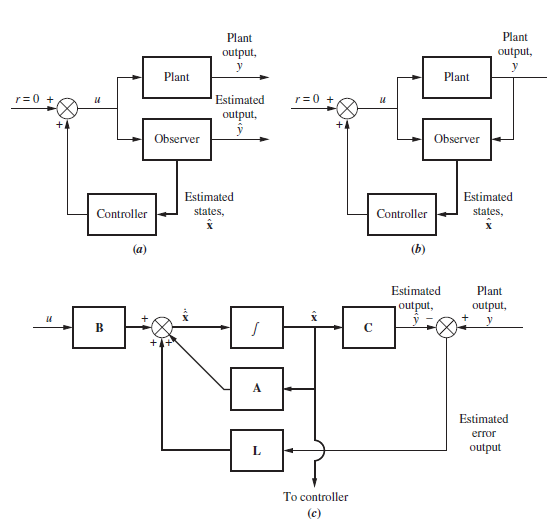
Partiendo de la ecuación de estados para la planta y para el observador
\[\begin{align} \dot{x}&=A\,x+B\,u \\ y&=C\,x \end{align}\] \[\begin{align} \dot{\hat{x}}&=A\,x+B\,u+L(y-\hat{y}) \\ \hat{y}&=C\,x \end{align}\]substrayendo las ecuaciones anteriores:
\[\begin{align} \left(\dot{x}-\dot{\hat{x}}\right)&=A\,\left(x-\hat{x}\right)-L(y-\hat{y}) \\ \left(y-\hat{y}\right)&=C\,\left(x-\hat{x}\right) \end{align}\]sustituyendo la ecuación de salida en la ecuación de estado:
\[\begin{align} \left(\dot{x}-\dot{\hat{x}}\right)&=(A-LC)\,\left(x-\hat{x}\right) \\ \left(y-\hat{y}\right)&=C\,\left(x-\hat{x}\right) \end{align}\]definiendo $e_x = \left(x-\hat{x}\right)$ tendremos:
\[\begin{align} \dot{e_x}&=(A-LC)\,e_x \\ \left(y-\hat{y}\right)&=C\,e_x \end{align}\]Control Integral
Diagrama completo con control integral.
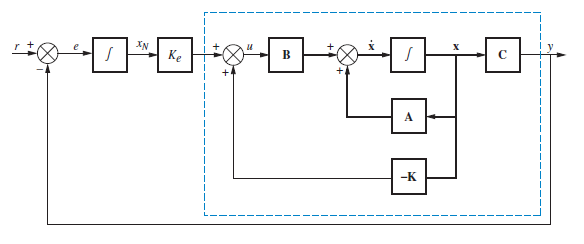
se desarrolla una representación en espacio de estados con la nueva variable y se define el valor de $K_e$.
\[\begin{align} \begin{bmatrix} \dot{x}\\ \dot{x_N} \end{bmatrix}&= \begin{bmatrix} (A-BK) & B\,K_e \\ -C & 0 \end{bmatrix} \,\begin{bmatrix} x\\ x_N \end{bmatrix}+ \begin{bmatrix} 0\\ 1 \end{bmatrix} \,r \\ y&= \begin{bmatrix} C & 0 \end{bmatrix} \,\begin{bmatrix} \dot{x}\\ \dot{x_N} \end{bmatrix} \end{align}\]Ejercicios
Considerando la siguiente representación en espacio de estados:
\[\begin{align} \dot{x}&= \begin{bmatrix} 0 & 1 \\ -3 & -5 \end{bmatrix} \,x+ \begin{bmatrix} 0\\ 1 \end{bmatrix} \,u \\ y&= \begin{bmatrix} 1 & 0 \end{bmatrix} \,x \end{align}\]- Diseñar un controlador sin control integral que genere un sobre pico del $10\%$ y un tiempo de establecimiento de $0.5$ segundos. Evaluar el error en estado estacionario para un escalón unitario.
- Repita el diseño del controlador incluyendo el control integral. Evaluar el error en estado estacionario para un escalón unitario.
Referencias
Nise, Norman S. Sección 12. Control systems engineering (7th Ed).